Tip: Start typing in the input box for immediate search results from our Resources Knowledge Base.
For a more comprehensive search, use the site search in the main menu above.
Manuals & Operating Instructions | Contact Support
Tips and tricks to master the Advanced Boolean Expression
by Jose Raul Naranjo
Introduction
The ABE formalism uses logical operators and predefined functions to effectively perform conditional segmentation in BrainVision Analyzer 2. It is especially useful when segmentation relative to a marker depends on its temporal location in a non-trivial sequence of other markers. It is not always clear how to construct the logical expressions underlying the ABE. In this article I would like to offer some tips and tricks that may help to understand important aspects of ABE formalism and discuss a couple of examples. It would be helpful if the reader is familiar with the basic syntax of the ABE formalism. More information can be found in Appendix J “Segmentation using advanced Boolean expressions” of the User Manual as well as the article “Did you know how to select the correct responses in BrainVision Analyzer 2?”, published in the Press Release 2/2010 (www.brainproducts.com/filedownload.php?path=pressrelease/BPPR_0210_35.pdf ).
Common difficulties when constructing an ABE
Typical experimental designs in neurophysiological research have a simple event structure (e.g. stimulus-response paradigm). However, depending on the various aspects that characterize the paradigm, the ABE may become more complex. At least three common difficulties should be taken into account.
1. The sequence of markers
Segments should be extracted relative to a marker, but only if this marker is located within a predefined marker sequence. For instance, the ABE should select markers S1 only if located in the sequence [S1 S2 S3]. Thus, sequences such as [S1 S2 S4] or [S1 S3 S2] should be excluded.
2. The time window
The time window where markers should appear (between times t1 and t2) may be fixed a-priori by the researcher. Thus, trials that do not fit to these temporal constraints are simply excluded. However, if all available trials should be included and the trial length varies widely (e.g. from dozens of milliseconds to several seconds), the values for t1 and t2 are data-dependent and thus cannot be fixed a-priori.
3. Local and global criteria
Segments should be extracted relative to a marker S1 only if both local and global criteria are met. For example, in the stimulus response sequence [S2 R2 S1 R1 S1 R2] [F1], the stimulus marker S1 should be selected if it is followed by the response marker R1 (local criterion), and if the whole sequence is then followed by the marker F1 (global criterion).
In the next sections, I will discuss two examples showing the difficulties mentioned above, and I will show how the ABE formalism can be used to overcome them.
Example 1: Marker sequences in a stimulus-response paradigm
In experimental designs where stimulus-response compatibility plays a role (e.g., Simon task or Stroop test), participants’ responses are prone to errors in an incongruent situation. Therefore, separation of correct and incorrect trials may be of interest. Let’s assume that only two stimuli S1 and S2 and their corresponding responses R1 and R2 are involved. Participants are requested to respond as quickly and as accurately as possible after the stimulation and are allowed to correct their responses within the time available for this trial. In this design, eight different sequences of events can be observed as shown in the Figure 1.
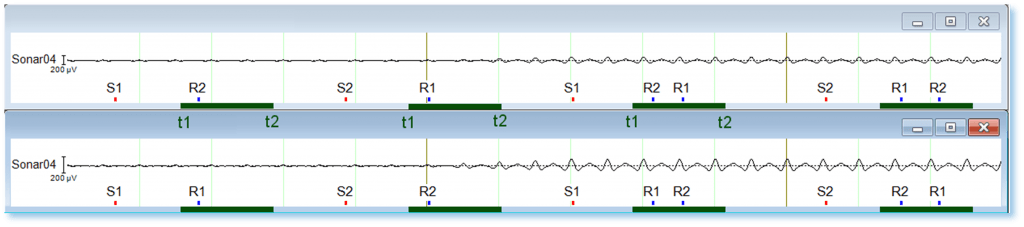
Figure 1: Eight possible marker sequences in simulated data. The green bars denote the time interval (t1,t2) in which response markers should appear to be selected.
The ABE formalism is able to differentiate between these eight different sequences if the time values t1 and t2 (green bars in Figure 1) and the marker sequence are specified. Classification of the eight sequences can be better understood if pooled as shown in Table 1 and Figure 2 below.
| Pools | Description |
|---|---|
| A | Purely correct trials |
| B | Trials containing a first correct and a second incorrect response marker |
| C | Purely incorrect trials |
| D | Trials containing a first incorrect and a second correct response marker |
Table 1: Description of the four pools of trials
In Figure 2A, sequences [S1 R1] and [S2 R2] indicate those trials where participants responded only once and correctly. Figure 2B contains the sequences [S1 R1 R2] and [S2 R2 R1], where participants correctly responded the first time, but added a second incorrect response. This case is atypical but theoretically possible, and thus researchers may wish to differentiate between ‘purely correct’ trials A and trials B. In Figure 2C, participants responded only once and incorrectly as seen in the sequences [S1 R2] and [S2 R1]. In Figure 2D participants responded a second time to correct their incorrect response, as seen in the sequences [S1 R2 R1] and [S2 R1 R2]. Similarly, it would be of interest to distinguish ‘purely incorrect’ trials C from corrected trials D.
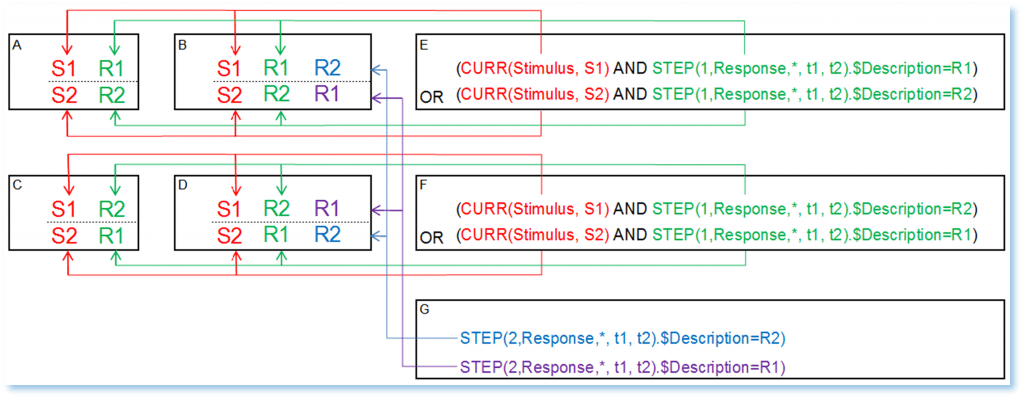
Figure 2: Four pools of trials A, B, C, and D and their corresponding ABEs
Let’s first focus on those trials where stimulus markers are followed by their corresponding response markers ([S1 R1…], [S2 R2…]), i.e. participants responded correctly the first time (Pools A and B).
When segmenting relative to stimulus S1 (i.e. S1 is the reference marker), the ABE is:
(CURR(Stimulus, S1) AND FIRST(Response,*, t1, t2).$Description=R1)
where t1 and t2 are the beginning and end of the time interval where the response markers should be selected, as indicated by green bars in Figure 1.
The expression FIRST(Response,*, t1, t2).$Description=R1) checks if the first response marker in the interval (t1,t2) is labelled as R1. Note that the function FIRST is just a particular case of the function STEP, which is able to evaluate a Boolean expression at any position in the marker sequence. The equivalent expression in terms of the function STEP would be STEP(1,Response,*, t1, t2).$Description=R1).
As shown in Figure 2E, the ABE for both stimuli S1 and S2 is:
(CURR(Stimulus, S1) AND STEP(1,Response,*, t1, t2).$Description=R1) OR
(CURR(Stimulus, S2) AND STEP(1,Response,*, t1, t2).$Description=R2)
In this expression, the CURR function selects, if available, the stimulus markers S1 or S2, and the STEP function checks simultaneously if, in the list of all existing response markers in the interval (t1, t2), the first marker is labelled R1 or R2. The logical operator AND implies the simultaneity of searching operations. The logical operator OR is used to apply the same procedure for both stimuli S1 and S2. Note that the position value 1 in “STEP(1,…)” is positive, meaning that the search through the markers is carried out forwards (i.e. from left to right) in the interval (t1,t2).
As shown in Figure 2F, in order to extract trials C and D, you just need to adapt the expression above, i.e. to exchange the response markers labels within the STEP function.
It is important to note that the ABEs in Figure 2E and 2F do not enquire if there is a second event after the first correct/incorrect response (as in pools B and D). In order to identify those pools, another ABE focusing on the existence of a second response marker R1 or R2 is needed.
As shown in Figure 2G, these expressions are:
STEP(2,Response,*,t1,t2).$Description=R2
STEP(2,Response,*,t1,t2).$Description=R1
Thus, to extract the pool of corrected trials D, the resulting ABE should be:
(CURR(Stimulus, S1) AND STEP(2,Response,*, t1, t2).$Description=R1) OR
(CURR(Stimulus, S2) AND STEP(2,Response,*, t1, t2).$Description=R2)
Note that by the design of this experiment, a correct second response automatically implies that the first response was incorrect (and vice versa).
By the same logic, in order to isolate ‘purely incorrect’ trials C it is mandatory to exclude pool D, i.e. to add a negation to the STEP function using the logical operator NOT. The resulting ABE for pool C is then:
(CURR(Stimulus, S1) AND NOT(STEP(2,Response,*, t1, t2).$Description=R1)) OR
(CURR(Stimulus, S2) AND NOT(STEP(2,Response,*, t1, t2).$Description=R2))
Let’s now discuss how to perform a segmentation relative to the response markers R1 or R2. As shown in Figure 3 below, in order to extract segments from trials A and B, the ABE needs to search to the left of response markers R1 and R2 for their corresponding stimulus markers S1 and S2. Besides, it should not enquire about the existence of any marker to the right of the response markers. This is achieved with the ABE:
(CURR(Response, R1) AND STEP(-1,Stimulus,*, -t2,-t1).$Description=S1) OR
(CURR(Response, R2) AND STEP(-1, Stimulus,*,-t2,-t1).$Description=S2)

Figure 3: ABE for segmenting trials in pools A and B relative to response markers R1 and R2
Note that in this case the position value -1 in “STEP(-1,…)” is negative, meaning that the search in the list of all possible stimulus markers is carried out backwards (from right to left) in the time interval (-t2,-t1).
As already mentioned, if the trial length varies widely and all available trials should be included, t1 and t2 values are data-dependent. The critical issue is how to specify the values t1 and t2 in the ABE if they are not known a-priori.
In Figure 4 below, three different trials from the stimulus response paradigm are shown. In the middle panel a given time interval T between stimulus S2 and response marker R2 is represented. The upper and lower panels show the minimal and maximal values of the interval T across all trials/conditions/participants.
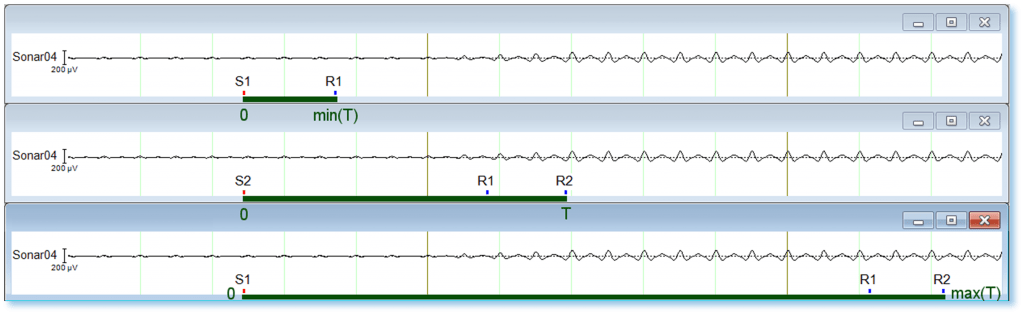
Figure 4: Three different time intervals (green bars) between stimulus marker and response marker.
In order to include all trials, if segmentation is, for example, relative to the stimuli S1 or S2, it is necessary that t1 is smaller than the minimum interval T and t2 larger than the maximum interval T. As those values are difficult to estimate visually, a good strategy would be to set min(T) to 0 ms and max(T) to any large number of ms (e.g. 60 000 ms, if no trial is longer than one minute).
Note that the time interval (t1, t2) is not limited to the length of the segment that will be defined at the third window of the segmentation wizard in Analyzer 2.
Example 2: How to handle local and global criteria
In order to identify local and global features of marker sequences, let’s introduce a new experimental paradigm with two categories of visual stimuli, i.e. faces (F) and houses (H). Stimuli may also appear with two possible orientations, i.e. upwards (Fu, Hu) and downwards (Fd, Hd). Each trial includes three stimulus-response pairs (S-R), i.e. three stimuli of the same category, each followed by a response marker to report stimulus orientation as upwards (Ru) or downwards (Rd), independently of the category of the visual stimulus. Each trial/sequence is then followed by a second response marker to report the stimulus category, i.e. if all stimuli in a trial are faces (F) or houses (H). Four possible trials are shown in Figure 5. A schematic representation of the same four trials is shown in Figure 6.
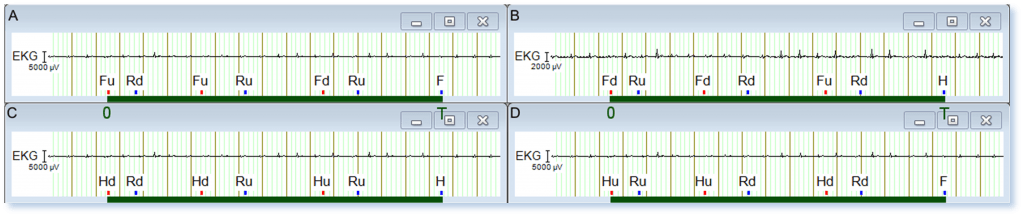
Figure 5: Four possible trials/marker sequences in recorded data. The green bar denotes a time interval (0, T) where the whole trial is included.
Figure 5A shows the face sequence [Fu Rd Fu Ru Fd Ru] [F]. It contains one correct (Fu Ru) and two incorrect (Fu Rd, Fd Ru) (S-R) pairs, which are represented as (ud, uu, du) in Figure 6A. As the stimulus category face (F) was correctly reported by the response marker F, the whole sequence is labeled as FF, as shown in Figure 6A. Similarly, the house sequence [Hu Ru Hu Rd Hd Rd] [F] in Figure 5D contains two correct and one incorrect (S-R) pairs, and is represented as (uu, ud, dd) in Figure 6D. As the stimulus category house (H) was incorrectly reported by the response marker F, the whole sequence is labelled as HF.
According to the schematic description in Figure 6, the local criterion in this paradigm refers to each individual (S-R) pair, and evaluates whether participants responded correctly (uu, dd) or incorrectly (ud, du) while reporting the stimulus orientation. The global criterion refers to the whole trial or marker sequence, and evaluates whether participants responded correctly (FF, HH) or incorrectly (FH, HF) while reporting the stimulus category.
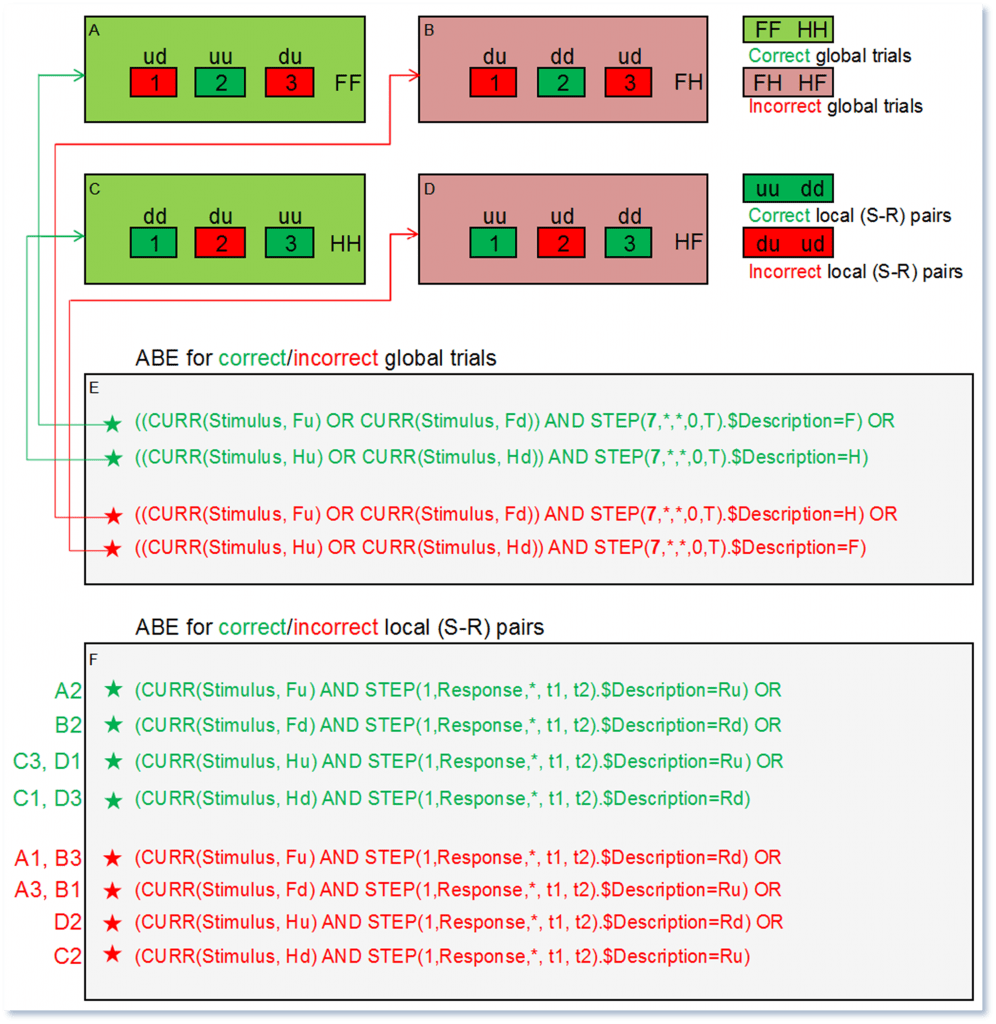
Figure 6: Schematic representation of four possible trials/marker sequences (A, B, C and D). Numbered green and red boxes represent the correct and incorrect (S-R) pairs within each trial. For instance, (S-R) pairs A1, D2, and B3 are the incorrect (S-R) pair ud. ABEs corresponding to the global and local criteria are shown in E and F.
If one is interested in extracting segments in which the stimuli orientation is indicated either correctly or incorrectly, then only the local criterion should be used, i.e. the response markers F and H should not be taken into account.
As shown in Figure 6F, when segmenting relative to all stimuli, the ABE for correct (S-R) pairs is:
(CURR(Stimulus, Fu) AND STEP(1,Response,*, t1, t2).$Description=Ru) OR
(CURR(Stimulus, Fd) AND STEP(1,Response,*, t1, t2).$Description=Rd) OR
(CURR(Stimulus, Hu) AND STEP(1,Response,*, t1, t2).$Description=Ru) OR
(CURR(Stimulus, Hd) AND STEP(1,Response,*, t1, t2).$Description=Rd)
where t1 and t2 define the time interval in which the response markers (Ru and Rd) should be selected.
When aiming for incorrect trials, you need to adapt the expression above, i.e. to exchange the response marker labels in the STEP function.
If one is interested in extracting segments relative to all stimuli while taking into account the correct/incorrect detection of the stimulus category (global criterion), then it is convenient to first extract segments containing the whole trial.
For instance, to extract all trials in which the stimulus category was correctly identified (as shown in Figure 5A,C and 6A,C), the seventh response marker (F or H, respectively) should match either the first face or house marker in the sequence.
As shown in Figure 6E, to extract correct trials relative to the first marker in the sequence, the appropriate ABE is:
((CURR(Stimulus, Fu) OR CURR(Stimulus, Fd)) AND STEP(7,*,*,0,T).$Description=F) OR
((CURR(Stimulus, Hu) OR CURR(Stimulus, Hd)) AND STEP(7,*,*,0,T).$Description=H)
where the time interval (0,T) should be large enough to include the whole marker sequence in every trial.
In order to extract all trials where the stimulus category was incorrectly identified, you need to adapt the expression above, i.e. to exchange the response markers F and H within the STEP function.
Note that the expression STEP(7,*,*,0,T).$Description=F will first create a list of all seven stimulus and response markers in the interval (0,T), and then check if the seventh or last marker, which reports the stimulus category, is labeled as F.
Once the four different pools of correct (A, C) and incorrect trials (B, D) are extracted, it is then appropriate to perform a second segmentation within each of the four pools of segmented data. The ABEs focusing on the local criterion can then be further applied to extract segments where the stimulus orientation was correctly/incorrectly detected, as shown in Figure 6F.
Concluding remarks
The ABE formalism has a very flexible structure to define logical statements regarding the temporal unfolding of the events sequence, as the ABE functions can be easily combined via logical operators. The examples included above cover typical applications where researchers encounter predefined marker orders, widely varying trial lengths, and the inclusion of both global and local criteria. If you are working with a sequence not covered in this article, we suggest that you first try to adapt the ABEs provided here and in the previously cited documents to your situation. If it remains difficult, feel free to contact our scientific support team with your questions.
Take-home messages
1. Create a scheme (e.g. similar to Table 1 and Figure 2A-D, 6A-D) with all cases of interest in your experimental design. This will help to construct ABEs for the different cases.
2. Once the ABEs pointing to each specific case are constructed, combine them in the proper order using the logical operators AND, OR and NOT.
3. The function STEP is a powerful tool to express predefined marker orders in a sequence. It is worth learning to use it!
4. Where the time window varies widely and all available trials should be included, estimate a time interval larger than all possible trials.
5. Avoid constructing an ABE which include both local and global criteria. After identifying local and global criteria in your marker sequence, separate the segmentation process accordingly. This will considerably simplify the ABE.
